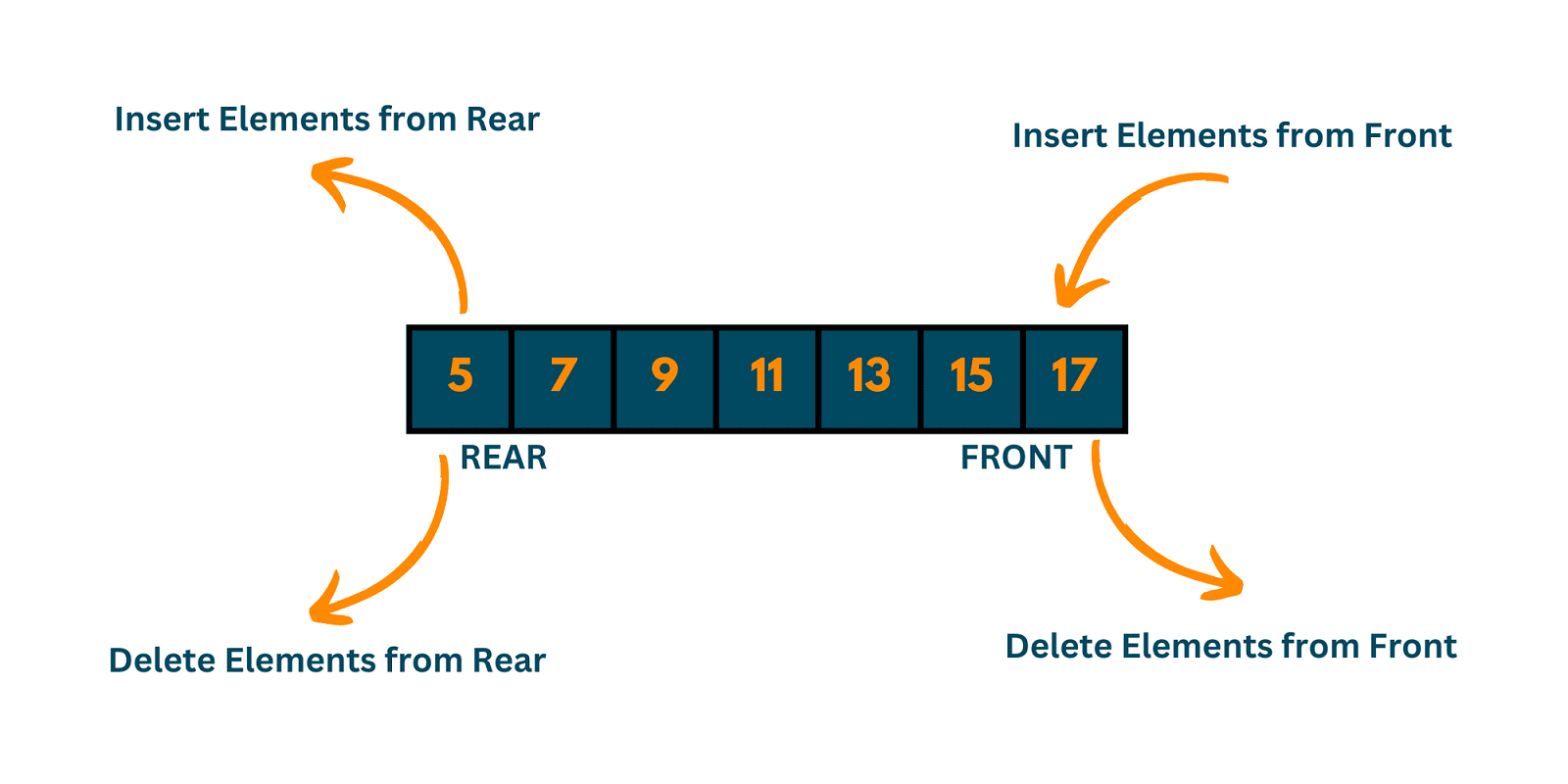
Python's collections module provides a powerful data structure called deque (pronounced "deck"), which stands for "double-ended queue." A deque is a generalization of stacks and queues, allowing you to add or remove elements from both ends efficiently. This makes it an excellent choice for scenarios where you need fast append and pop operations from both ends of the sequence.
In this article, we'll explore the deque data structure in detail, including its features, use cases, and how to use it effectively in your Python programs. We'll also provide code examples to illustrate its functionality.
What is Deque?
A Python dequeis a linear data structure that supports fast appends and pops from both ends. It is implemented as a doubly linked list, which allows for O(1) time complexity for append and pop operations at both the front and the back. This makes it more efficient than a list for certain operations, especially when dealing with large datasets.
Basic Concepts and Implementation
The deque class is part of Python's collections module, so you need to import it before using it:
from collections import deque# Create a new deque dq = deque(['a','b','c'])# Add elements to both ends dq.append('d')# Add to right dq.appendleft('z')# Add to leftprint(dq)# Output: deque(['z', 'a', 'b', 'c', 'd'])
This basic example demonstrates the creation and fundamental operations of a deque. We start by importing the deque class from Python's collections module and initialize it with three letters: 'a', 'b', and 'c'. Think of it as creating a two-way street where we can add vehicles (elements) from either end.
The append and appendleft operations showcase deque's key feature—bidirectional access. When we append('d'), it goes to the right end, like adding a car to the end of a queue. When we appendleft('z'), it goes to the left end, like someone cutting to the front of the line. This flexibility is what makes deque particularly useful for queue-based operations.
Key Operations and Their Time Complexity
The deque supports several efficient operations:
- Append/Pop Operations (O(1)):
dq = deque()
dq.append(1) # Add to right
dq.appendleft(2) # Add to left
dq.pop() # Remove from right
dq.popleft() # Remove from leftThe above snippets highlight the four primary operations available in a deque. These operations are crucial because they all operate in O(1) time complexity, meaning they execute in constant time regardless of the deque's size. It's like having instant access to both ends of a line of people.
The efficiency of these operations makes deque ideal for situations where you need frequent additions and removals at either end. For example, in a real-time system processing tasks, you could use appendleft to add high-priority tasks and append for normal priority tasks, while using pop/popleft to process them accordingly.
- Rotation Operations:
dq = deque([1, 2, 3, 4, 5])
dq.rotate(1) # Rotate right by 1
print(dq) # Output: deque([5, 1, 2, 3, 4])
dq.rotate(-2) # Rotate left by 2
print(dq) # Output: deque([2, 3, 4, 5, 1])The rotation operations in deque offer a unique way to shift all elements in a circular fashion. When we rotate(1), it's like taking the last element and moving it to the front - imagine a circular card deck where you move the bottom card to the top. This operation is particularly useful in scenarios where you need to cycle through elements in a circular manner.
Negative rotations work in the opposite direction. When we rotate(-2), it's like taking the first two elements and moving them to the end. This is incredibly efficient compared to doing the same operation with a regular list, as deque is optimized for these kinds of operations. Think of it as moving the first two cards in a deck to the bottom - it happens in one smooth motion rather than individual moves.
Practical Applications
-
Buffer Implementation
defcreate_buffer(size):return deque(maxlen=size)# Create a fixed-size bufferbuffer= create_buffer(3)for i inrange(5):buffer.append(i)print(buffer) # Only keeps last 3 elements
A fixed-size buffer, implemented using deque's maxlen parameter, creates a self-managing container that automatically discards old elements when it reaches capacity. This is like having a parking lot with a fixed number of spaces - when full, the oldest car must leave before a new one can enter. This becomes particularly useful in scenarios like maintaining a running window of recent data.
In this example, even though we add five numbers, the buffer only keeps the last three because of its maxlen property. When we append the fourth element, the first one is automatically removed. This automatic maintenance makes it perfect for applications like maintaining recent history, implementing caches, or processing streaming data where you only care about the most recent n items.
-
Task Queue Management
defprocess_tasks():tasks = deque(['task1','task2','task3'])while tasks:current_task = tasks.popleft()print(f"Processing {current_task}")
-
Sliding Window Problems
defsliding_window_max(arr, k):dq = deque()result =[]for i inrange(len(arr)):# Remove elements outside current windowwhile dq and dq[0]< i - k +1:dq.popleft()# Remove smaller elementswhile dq and arr[dq[-1]]< arr[i]:dq.pop()
dq.append(i)
# Add to result if window has reached size kif i >= k -1: result.append(arr[dq[0]])return result
This algorithm solves the maximum sliding window problem, a common interview question and real-world scenario. The deque is used to maintain indices of potentially maximum values in the current window. As the window slides, elements that fall outside the window are removed from the left, and elements smaller than the current element are removed from the right.
The beauty of this solution lies in its efficiency. While a naive approach would require O(nk) time (where n is array length and k is window size), this deque-based solution achieves O(n) time complexity. Think of it as maintaining a "smart" window that automatically tracks the maximum value while sliding through the array.
Advanced Features
-
Extended Iteration
dq = deque([1, 2, 3], maxlen=5)# Extend with multiple elementsdq.extend([4, 5])dq.extendleft([0, -1]) # Note: adds in reverse order
-
Count and Remove Operations
dq = deque([1, 2, 2, 3, 2])count = dq.count(2) # Count occurrencesdq.remove(2) # Remove first occurrence
The count method efficiently counts the number of occurrences of a specific element in the deque. This is useful when you need to track the frequency of elements without converting the deque to another data structure. It's like counting how many times a specific card appears in a deck.
When Should You Use Deque
Deque is particularly useful when you need:
- O(1) time complexity for append/pop operations at both ends
- A fixed-size buffer with automatic removal of old elements
- Implementation of sliding window algorithms
- Queue or stack functionality with additional features
Performance Considerations
-
Memory Usage:
from sys import getsizeofdq = deque(range(1000))list_obj = list(range(1000))print(f"Deque size: {getsizeof(dq)} bytes")print(f"List size: {getsizeof(list_obj)} bytes")
-
Operation Speed Comparison:
from timeit import timeit# Compare insertion at beginningdeque_time = timeit('dq.appendleft(1)', 'from collections import deque; dq=deque()') list_time = timeit('lst.insert(0, 1)', 'lst=[]')
Best Practices
-
Use maxlen for Fixed-Size Buffers:
# Create a circular buffercircular_buffer = deque(maxlen=3)for i in range(5):circular_buffer.append(i)# Only keeps last 3 elements
-
Clear Contents Efficiently:
dq = deque([1, 2, 3, 4, 5])dq.clear() # More efficient than dq = deque()
Common Pitfalls to Avoid
-
Avoid using index-based operations extensively:
# Less efficient for large dequesdq = deque(range(1000))middle_element = dq[len(dq)//2] # O(n) operation
-
Be careful with rotation on empty deques:
dq = deque()try:dq.rotate(1) # Works fine on empty dequedq.pop() # Raises IndexErrorexcept IndexError:print("Cannot pop from empty deque")
The deque data structure in Python provides a powerful and efficient way to handle double-ended queues. Its implementation in the collections module makes it a go-to choice for many algorithms and data processing tasks where quick insertion and deletion at both ends are required.